A Quick Guide to Confounding Factors
Posted on: June 17, 2022
Post Category: Statistics
Imagine you have a model.
From the results, you see that an increase in variable A corresponds to an increase in variable B.
And so you believe that an increase in variable A will cause an increase in variable B.
But what if it’s purely a correlation relationship and not a causation one?
If that’s the case, then there must be a hidden confounding factor that is causing the increase in that variable B.
Earlier this week, I wrote a post about a statistical perspective into twin studies, which involved a breakdown of epidemiological twin studies using the concept of confounding factors. Some of the content in this post will be repeated in there. You can read more about it here.
What are confounding factors?
Confounding factors are significant factors/effects that are not measured in an experiment or model. It can be thought of a third or extra variable(s) that mitigates a cause-and-effect relationship between our independent variable (i.e. the factor being studied) and dependent variable (i.e. what we are measuring as a result).
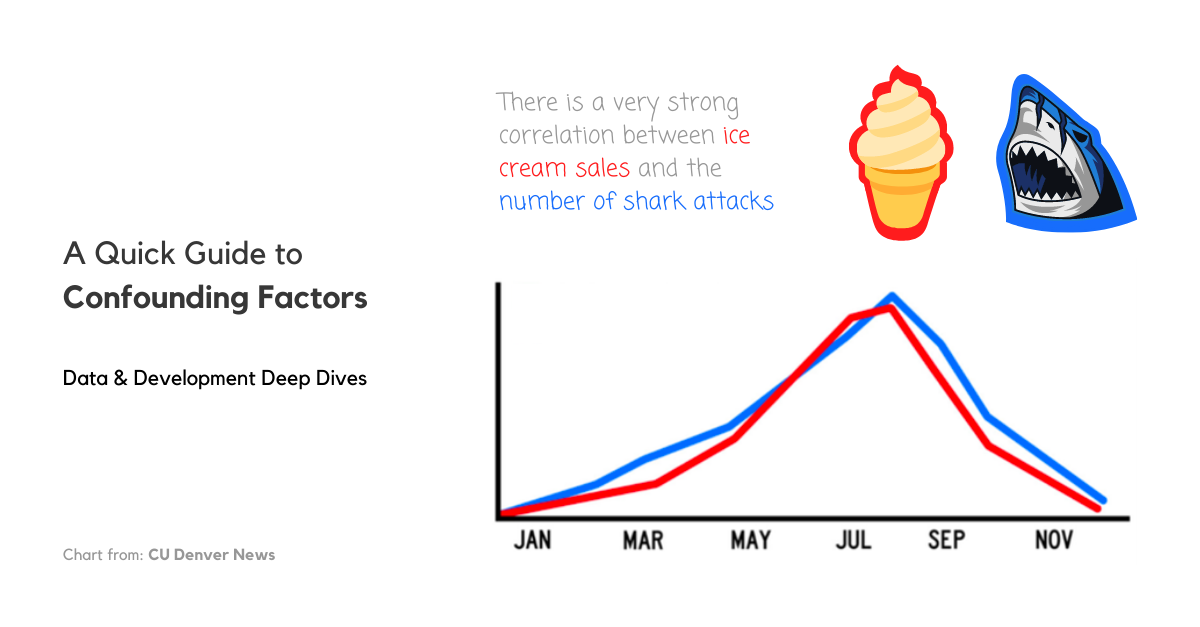
The classic ice cream sales and shark attacks example
A classic example to illustrate confounding factors is the significant correlation between ice cream sales and shark attacks. When ice cream sales increase, the number of shark attacks increase. Does that mean that ice cream sales cause shark attacks? No. The significant correlation is not because of a causation relationship but there is a confounding factor that links both variables: the temperature.
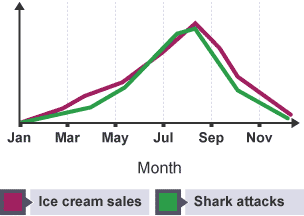
So, if we were to model the number of shark attacks using ice cream sales, an increase in ice cream sales would correspond to an increase in the number of shark attacks. BUT if we were to model the number of shark attacks using ice cream sales AND the temperature, an increase in ice cream sales, while holding the temperature constant/unchanged, will NOT increase the number of shark attacks – it will probably also be constant/unchanged.
While both models are correct, the second model better-highlights the underlying factors that cause shark attacks.
Another example – on the likelihood/risk of loan default
In ‘An Introduction to Statistical Learning with Applications in R (Second Edition)’, by Gareth James and his co-authors, a dataset on loan default was analysed.
Two models were compared: one modelled the default outcome using just the individuals’ student status, and the other modelled the default outcome using their student status, credit card balance and income.
The results are shown below:
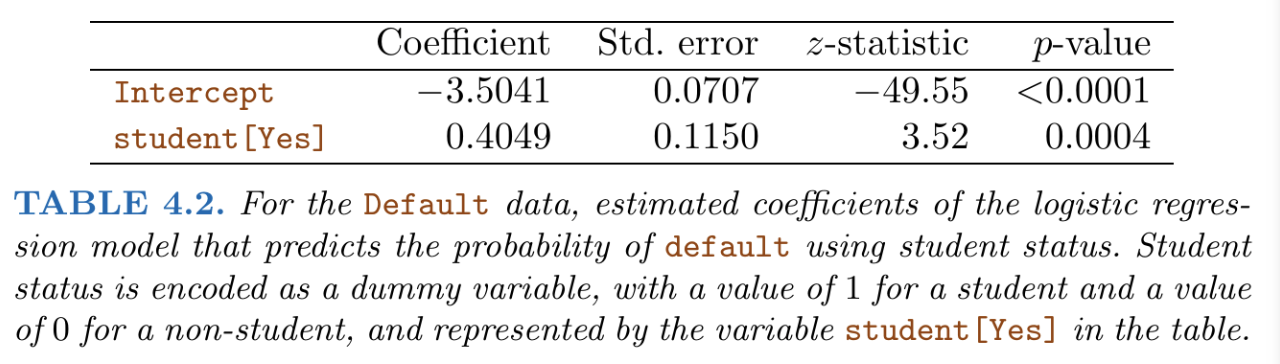
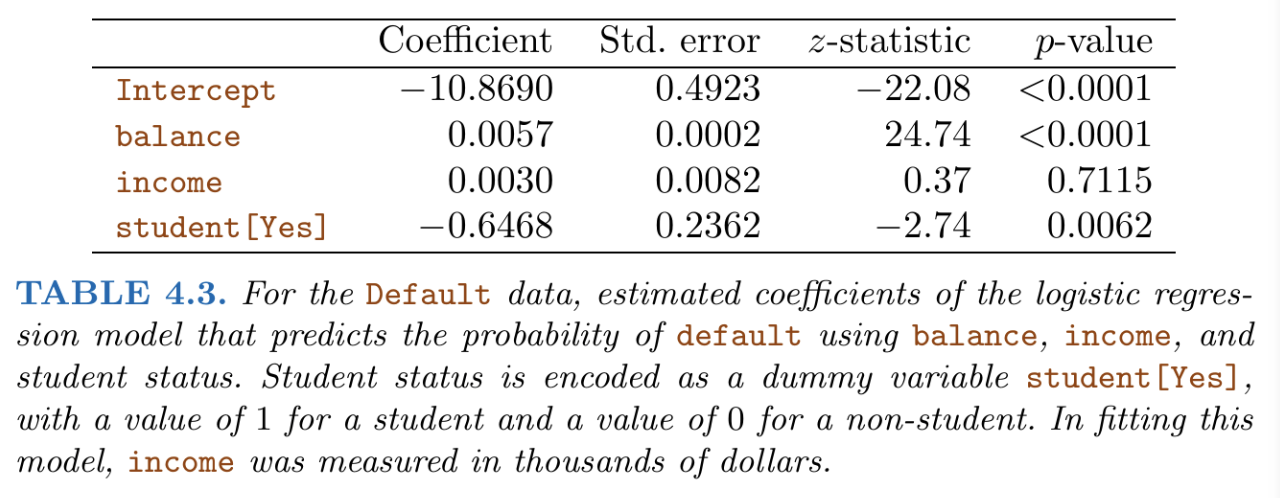
One peculiar thing you may notice is that from our first set of results, ‘student [Yes]’ (i.e. being a student) has a positive effect on the default rate (i.e. the risk of default), while from our second set of results, being a student has a negative effect on the default rate.
Why is this happening? This is because credit card balance and income are (hidden) confounding factors that cause the ‘student [Yes]’ variable to have a positive effect on the default rate. In particular, students tend to have higher levels of debt, and higher levels of debt is associated with higher default risk.
To illustrate this difference more clearly:
- For our first model, the results show that the default rate for students is higher than non-students, if we were to average over all values of credit card balance and income.
- For our second model, the results show that the default rate for students is lower than non-students, at a fixed level of credit card balance and income.

About the author
Jason Khu is the creator of Data & Development Deep Dives and currently a Data Analyst at Quantium.